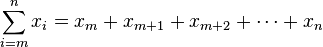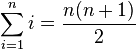Introducción
La palabra cálculo proviene del latín calculus, que significa contar con piedras. Precisamente desde que el hombre ve la necesidad de contar, comienza la historia del calculo, o de las matemáticas.
Las matemáticas son una de las ciencias más antiguas, y más útiles. El concepto de matemáticas, se comenzó a formar, desde que el hombre vio la necesidad de contar objetos, esta necesidad lo llevó a la creación de sistemas de numeración que inicialmente se componían con la utilización de los dedos, piernas, o piedras. De nuevo, por la necesidad, se hizo forzosa la implementación de sistemas más avanzados y que pudieran resolver la mayoría de los problemas que se presentaban con continuidad.
Las matemáticas son una de las ciencias más antiguas, y más útiles. El concepto de matemáticas, se comenzó a formar, desde que el hombre vio la necesidad de contar objetos, esta necesidad lo llevó a la creación de sistemas de numeración que inicialmente se componían con la utilización de los dedos, piernas, o piedras. De nuevo, por la necesidad, se hizo forzosa la implementación de sistemas más avanzados y que pudieran resolver la mayoría de los problemas que se presentaban con continuidad.
La historia del cálculo, comienza desde que comenzó la historia del hombre, cuando este vio la necesidad de contar
Han sido muchos los grandes matemáticos que han influido en el desarrollo que actualmente posee el calculo, igualmente que han sido muchas las culturas que han influido en sus avances
Las matemáticas, actualmente son la base de todas las ciencias que maneja el hombre, debido a que su campo de acción cubre la totalidad de los conocimientos científicos.
¿Que es el calculo diferencial?
El cálculo diferencial es una parte importante del análisis matemático y dentro del mismo del cálculo. Consiste en el estudio del cambio de las variables dependientes cuando cambian las variables independientes de las funciones o campos objetos del análisis. El principal objeto de estudio en el cálculo diferencial es la derivada. Una noción estrechamente relacionada es la de diferencial de una función.
En el estudio del cambio de una función, es decir, cuando cambian sus variables independientes es de especial interés para el cálculo diferencial el caso en el que el cambio de las variables es infinitesimal, esto es, cuando dicho cambio tiende a cero (se hace tan pequeño como se desee). Y es que el cálculo diferencial se apoya constantemente en el concepto básico del límite. El paso al límite es la principal herramienta que permite desarrollar la teoría del cálculo diferencial y la que lo diferencia claramente del álgebra.
Desde el punto de vista matemático de las funciones y la geometría, la derivada de una función en un cierto punto es una medida de la tasa en la cual una función cambia conforme un argumento se modifica. Esto es, una derivada involucra, en términos matemáticos, una tasa de cambio. Una derivada es el cálculo de las pendientes instantáneas de
en cada punto 
. Esto se corresponde a las pendientes de las tangentes de la gráfica de dicha función en sus puntos (una tangente por punto); Las derivadas pueden ser utilizadas para conocer la concavidad de una función, sus intervalos de crecimiento, sus máximos y mínimos.La inversa de una derivada se llama primitiva, antiderivada o integral indefinida.
Algunos autores importantes en el calculo diferencial
El Cálculo constituye una de las grandes conquistas intelectuales de la humanidad. Una vez construído, la historia de la matemática ya no fue igual: la geometría, el álgebra y la aritmética, la trigonometría, se colocaron en una nueva perspectiva teórica. Detrás de cualquier invento, descubrimiento o nueva teoría, existe, indudablemente, la evolución de ideas que hacen posible su nacimiento. Es muy interesante prestar atención en el bagaje de conocimientos que se acumula, desarrolla y evoluciona a través de los años para dar lugar, en algún momento en particular y a través de alguna persona en especial, al nacimiento de una nueva idea, de una nueva teoría, que seguramente se va a convertir en un descubrimiento importante para el estado actual de la ciencia y, por lo tanto merece el reconocimiento. El Cálculo cristaliza conceptos y métodos que la humanidad estuvo tratando de dominar por más de veinte siglos. Una larga lista de personas trabajaron con los métodos "infinitesimales" pero hubo que esperar hasta el siglo XVII para tener la madurez social, científica y matemática que permitiría construir el Cálculo que utilizamos en nuestros días.
Sus aplicaciones son difíciles de cuantificar porque toda la matemática moderna, de una u otra forma, ha recibido su influencia; y las diferentes partes del andamiaje matemático interactúan constantemente con las ciencias naturales y la tecnología moderna.
Newton y Leibniz son considerados los inventores del cálculo pero representan un eslabón en una larga cadena iniciada muchos siglos antes. Fueron ellos quienes dieron a los procedimientos infinitesimales de sus antecesores inmediatos, Barrow y Fermat, la unidad algorítmica y la precisión necesaria como método novedoso y de generalidad suficiente para su desarrollo posterior. Estos desarrollos estuvieron elaborados a partir de visiones de hombres como Torricelli, Cavalieri, y Galileo; o Kepler, Valerio, y Stevin. Los alcances de las operaciones iniciales con infinitesimales que estos hombres lograron, fueron también resultado directo de las contribuciones de Oresme, Arquímedes y Eudoxo. Finalmente el trabajo de estos últimos estuvo inspirado por problemas matemáticos y filosóficos sugeridos por Aristóteles, Platón, Tales de Mileto, Zenón y Pitágoras. Para tener la perspectiva científica e histórica apropiada, debe reconocerse que una de las contribuciones previas decisivas fue la Geometría Analítica desarrollada independientemente por Descartes y Fermat.
Sin la contribución de éstos y de muchos otros hombres más, el cálculo de Newton y Leibniz seguramente no existiría. Su construcción fue parte importante de la revolución científica que vivió la Europa del siglo XVII.Los nuevos métodos enfatizaron la experiencia empírica y la descripción matemática de nuestra relación con la realidad. La revolución científica supuso una ruptura con las formas de pensar, estudiar y vincularse con la naturaleza que dominaron casi absolutamente en Europa entre los siglos V y XV. Esta ruptura y salto en la historia del conocimiento estuvieron precedidos por las importantes transformaciones que se vivieron durante los siglos XV y XVI con el Renacimiento y la Reforma Protestante. El Cálculo Diferencial e Integral están en el corazón del tipo de conocimiento, cultura y de sociedad de la que, esencialmente, somos parte.
El extraordinario avance registrado por la matemática, la física y la técnica durante los siglos XVIII, XIX y XX, se lo debemos al Cálculo infinitesimal y por eso se puede considerar como una de las joyas de la creación intelectual de la que el hombre puede sentirse orgulloso.
MINIBIOGRAFIAS DE ALGUNOS MATEMÁTICOS
Zenón de Elea (c. 490 a.C- c. 430 a.C.)
Principal discípulo de Parménides, cuyo pensamiento defendió mediante sus famosas aporías (“paradojas”), con las cuales reducía al absurdo las tesis que pretendía demostrar. Por ello Aristóteles le consideró el creador de la dialéctica.
Diofanto (c. 325- c.410)
Matemático griego de la escuela de Alejandría.
Redactó trece libros de aritmética y uno de números angulares. Desarrollo una teoría innovadora acerca de las ecuaciones de primer grado y propuso formas de resolución de las de segundo grado.
Euclides (c.3000 a. C)
Matemático griego fundador de la escuela de Alejandría. Además de sus aportaciones a otros campos del saber como la óptica, su principal obra fue llamada Elementos, considerada la obra de geometría por excelencia, y que contiene el famoso postulado que lleva su nombre.
Arquímedes (287 a. C.- 212 a. C.)
Sabio griego. Discípulo de Euclides, además de sus importantes de carácter físico (p.ej. las leyes de la palanca) y técnico (tornillo, sin fin, polea móvil, ruedas dentadas, etc.), desarrollo un método para obtener el número pi, perfeccionó el sistema numérico griego y realizo notables contribuciones en el campo de la geometría.
Eratóstenes (c. 284 a. C.- c.192 a.C.)
Astrónomo, filósofo, geógrafo y matemático. Además de ser el primero en medir de forma exacta la circunferencia de la Tierra, creó la criba que lleva su nombre, para la obtención de los números primos, y un instrumento para resolver el problema de la media proporcional (mesolabio).
Fermat, Pierre de (1601-1665)
Matemático francés. Se le reconoce el mérito de haber expresado las primeras idea acerca de cálculo diferencial y algunos autores le reconocen la paternidad del cálculo de probabilidades, compartida con Pascal. Entre sus creaciones destacan el principio, el teorema y el último teorema que llevan su nombre.
Pascal, Blaise (1623-1662)
Matemático, físico, filósofo y escritor francés. Aparte de importantes resultados en el estudio de las cónicas, cicloides y primeros esbozos del cálculo infinitesimal, se le deben contribuciones fundamentales en diversos campos de la física (estudio del vacío, estática de líquidos, etc.), la construcción de varios ingenios mecánicos de cálculo (pascalinas) y la formulación de las bases del cálculo de probabilidades.
Newton,sir Isaac (1642-1727)
Físico, matemático y astrónomo británico.
Sus importantes contribuciones a los campos de las matemáticas y la física incluyen, entre otros, el llamado cálculo de fluxiones (cálculo infinitesimal cuya paternidad le disputa Leibniz) y la sistematización de la mecánica clásica, así como la formulación de las leyes de la gravitación universal.
Goldbach, Christian (1690-1764)
Matemático alemán.sus trabajos se centraron en la teoría de series y sus aplicaciones a la integración de ecuaciones diferenciales. Planteó el problema que lleva su nombre (1742) y que fue resuelto en 1937 por Vinogradov, y propuso la conjetura de Goldbach, aún no resuelta.
Euler, Leonhard (1707-1783)
Matemático suizo.Fue el más famoso de la familia de matemáticos a la que perteneció.
Entre sus obras destacan su Tratado completo de mecánica (aplicación del análisis matemático al movimiento), su teoría del movimiento de los planetas y cometas y, sobre todo, su Introducción al análisis de infinitésimos (1748)y sus Instituciones de cálculo integral (1755), consideradas clásicas.
Clairaut. Alexis (1713-1765)
Matemático y astrónomo francés. Además de participar en la expedición a Laponia para la mediad del meridiano terrestre y calcular el regreso del cometa Halley (1758), hizo contribuciones a la llamada teoría de los tres cuerpos y, en el campo de las matemáticas, al llamado análisis superior.
Lagrange, conde Louis de (1736-1813)
Matemático francés. Además de sus aportaciones el cálculo de variaciones y al cálculo integral, como la introducción de un simbolismo más cómodo para éste, se le debe una obra fundamental titulada Mecánica analítica (1788)
Fundamentó el análisis sobre una noción más general de función, en particular mediante el empleo de desarrollos en serie de Taylor.
Definió las funciones derivadas e introdujo una notación especial para expresarlas.
Gauss, Carl- Friedrich (1777-1855)
Astrónomo, matemático y físico alemán.
Además de sus importantes trabajos en los campos de la astronomía y la física, escribió u tratado sobre la teoría de los números, ideó el método de los mínimos cuadrados, creó la teoría de errores hizo aportaciones notables en el campo de las curvas y desarrolló un método general de resolución de ecuaciones binomias.
Bolzano, Bernhard (1781-1848)
Filósofo, lógico y matemático checo de origen italiano. Además de sus importantes trabajos en el campo de los fundamentos de la lógica, anticipo importantes concepciones relativas a la teoría de conjuntos y creó la primera función continua no diferenciable en ningún punto.
Cauchy, barón Augustin (1789-1857)
Matemático francés. Autor de más de setecientas memorias en diversos campos de la ciencia, introdujo métodos rigurosos en el campo del análisis y creó la llamada teoría de las funciones analíticas.
Abel, Niels Henrik. (1802-1829)
En el campo del análisis matemático está considerado, junto con Jacobi, como el creador de la teoría de funciones elípticas. Formuló, en un trabajo presentado ante la Academia de Ciencias de París, el teorema que lleva su nombre.
Dirichlet, Gustav Lejeume (1805-1859)
Matemático alemán. Sus principales aportaciones (fundamentales para la física matemática) se refieren alas series e integrales trigonométricas y al campo de la teoría de ecuaciones en derivadas parciales, así como a una rama abstracta de las matemáticas como la teoría de los números.
Galois, Evariste (1811-1832)
Matemático francés, Formuló una teoría de las ecuaciones matemáticas, recogiendo los resultados relativos a la clasificación y periodicidad de las integrales abelianas. Su principal aportación se centra en la importancia de los grupos en la resolución de ecuaciones algebraicas.
Boole, George (1815-1864)
Lógico y matemático británico. Se le debe la introducción del cálculo algebraico en le campo de la lógica y el cálculo de clases conocido como algebra de Boole de las clases.
Heine, Heinrich Eduard (1821-1881)
Matemático alemán. Heine hizo sus principales contribuciones de las matemáticas en el campo del análisis (polinomios de Legendre, funciones de Bessel y Lamé, etc. Su resultado más famoso es el llamado teorema de Heine- Borel.
Kronecker, Leopold (1823-1891)
Matemático alemán. Considerado uno de los mayores algebristas del siglo XIX , estudió, entre otras las funciones elípticas en aritmética y la teoría de cuerpos de los números algebraicos.
Riemann, Georg Friedrich Bernhard (1826-1866)
Matemático alemán. Además de sus contribuciones a la física matemática, hizo aportaciones a la teoría de funciones y enunció los fundamentos de la geometría diferencial para espacios de dimensión superior a tres. Formuló la teoría de las funciones abelianas e introdujo la llamada función z, lo que permitió obtener resultados notables relativos a los números primos.
Dedekind, Richard (1831-1916)
Matemático alemán. Alumno de Gauss, e introductor en el campo del análisis de las nociones que permiten precisar el concepto de número inconmensurable, se le deben trabajos relativos, entre otros, a las integrales eulerianas, a los números irracionales, a las ecuaciones y funciones algebraicas, etc.
Frege, Gottlob (1848-1952)
Filósofo, lógico y matemático alemán. Considerado el fundador de la lógica moderna o matemática, cuyos trabajos tuvieron una notable influencia en pensadores como Carnap, Husserl y Wittgenstein.
Cantor, Georg (1854-1948)
Matemático alemán de origen ruso. Se le considera el creador de la llamada teoría de conjuntos y de la teoría de los números transfinitos. Su obra impulsó una revisión en profundidad de los fundamentos de las matemáticas.
Poincaré, Henri (1854-1912)
Matemático francés, es autor de contribuciones fundamentales en los campos de la teoría de funciones, las ecuaciones diferenciales y sus aplicaciones a los problemas de la mecánica celeste, y el estudio de problemas de física matemática(p. ej., teoría de las ondas electromagnéticas).
Peano, Giuseppe (1858-1932)
Lógico y matemático italiano. Además de la exposición rigurosamente deductiva de diversos campos de las matemáticas, creó un sistema de de símbolos para la descripción y enunciado de las proposiciones lógicas y matemáticas sin necesidad de recurrir al lenguaje ordinario.
Whitehead, Alfred North (1861-1947)
Filósofo y matemático británico. Además de sus fundamentales aportaciones en el campo de la filosofía, está considerado como uno de los de la lógica matemática.
Hilbert, David (1862-1943)
Matemático alemán. Se le debe la formulación de la noción de cuerpo y la creación de la teoría de los cuerpos para los números algebraicos. Desarrolló los fundamentos de la llamada teoría de invariantes y estableció las bases de la teoría de prototipos de polinomios. Sus fundamentos de geometría (1899) están considerados el punto de partida de la axiomatización de varias ramas de las matemáticas.
Hadamard, Jacques (1865-1963)
Matemático francés. En la vasta obra que produjo gracias a su longevidad, destacan sus importantes investigaciones relativas ala distribución de los números primos, al análisis funcional término acuñado por Hadamard), así como sus resultados relativos a la teoría de números.
De la Vallée- Pousin, Charles Jean Gustave Nicolas (1866-1692)
Matemático belga. Realizo importantes trabajos relativos a las ecuaciones diferenciales a la función z de Riemann y fue autor de un famoso curso de análisis. Su resultado más importante fue el teorema de los números primos.
Russel, Bertrad Arthur William tercerconde (1872-1970)
Filósofo matemático y sociólogo inglés. Creador del logicismo y de la llamada teoría de los tipos, además de sus aportaciones fundamentales a la filosofía del conocimiento, destacan sus contribuciones en los campos de la matemática, la filosofía de la ciencia, la teoría del conocimiento, etc.
Carathédory, Constantin (1873-1950)
Matemático grecogermano. Se le deben importantes contribuciones, entre otras, en los campos del cálculo de variaciones, la teoría de la medida y los problemas teóricos relacionados con las funciones.
Lebesque, Henri (1875-1941)
Matemático francés. Además de sus trabajos sobre teorías de funciones de variable real, es autor, entre otros logros, de una generalización de la noción de integral que lleva su nombre.
Hardy, G (odfrey). H (arold). (1877-1947)
Matemático Británico. Su vasta obra abarca la teoría de números, cuestiones de análisis puro y la teoría de funciones. En colaboración con Littlewood y Rosser obtuvo valores asintóticos para las series o productos finitos relacionados con los números primos, como por ejemplo la serie de sus inversos.
Fatuo, Pierre Joseph Louis (1878-1929)
Matemático francés. Además de sus estudios acerca de las series de Taylor y la integral de Lebesque, se le deben importantes trabajos relativos al movimiento planetario en medios resistentes.
Littlewood, John Edensor (1885-1977)
Matemático británico. Hizo aportaciones a la teoría de series, en colaboración con G.H Hardy, y público diversos trabajos basados en la aplicación del llamado método analítico Hardy- Littlewood- Ramanujan.
Ramanujan, Srinivasa (1887-1920)
Matemático indio. Con la ayuda de G.H Hardy se traslado a Inglaterra, donde escribió importantes artículos sobre la teoría analítica de los números. Sus descubrimientos tuvieron gran influencia en la física moderna (teoría de supercuerdas) y en el campo de la estadística de los sistemas moleculares.
Von Neuman, Johann o John (1903-1957)
Matemático estadounidense de origen húngaro. Fundamentalmente se le deben contribuciones muy notables a la teoría de conjuntos, a la teoría de juegos y al desarrollo de máquinas de calcular electrónicas.
Oppenheimer, Robert Julios (1904-1967)
Físico estadounidense. Realizó importante trabajos en los campos de la física atómica y la teoría cuántica. Dirigió la creación de la bomba atómica en Los Álamos (1943-1945).
Princeton (1947-1966) y se opuso a la construcción de la bomba de hidrógeno, por lo que obtuvo represalias.
Tichonov, Andréi Nikoláievich(1906-1993)
Matemático ruso. Destacó por sus trabajos en el campo de la topología y análisis funcional, en la teoría de ecuaciones diferenciales y en problemas de matemática computacional y física matemática.
Godel, kart (1906-1978)
Lógico estadounidense de origen austriaco. En su tesis relativa a los fundamentos lógico matemáticos, estableció la completitud del llamado cálculo de predicados. Si embargo, goza de fama mundial por la formulación de sus dos teoremas de incompletitud, que afirman que no puede demostrarse la completitud de la teoría matemática utilizando únicamente procedimientos formalizables en el seno de dicho sistema.
Weil, André (1906-1998)
Matemático francés. Contribuyó al avance de la geometría y la teoría de números estableciendo las bases de la geometría algebraica abstracta y de la moderna teoría de variedades abelianas . Sus trabajos sobre curvas algebraicas han tenido gran influencia incluso en la física moderna.
Turing. Alan Mathison (1912-1954)
Matemático británico. Hizo notables contribuciones en los campos de la lógica matemática, teoría de grupos, inteligencia artificial y máquinas de calcular. Se le debe asimismo la formulación de la llamada máquina de Turing.
Zenón de Elea (c. 490 a.C- c. 430 a.C.)
Principal discípulo de Parménides, cuyo pensamiento defendió mediante sus famosas aporías (“paradojas”), con las cuales reducía al absurdo las tesis que pretendía demostrar. Por ello Aristóteles le consideró el creador de la dialéctica.
Diofanto (c. 325- c.410)
Matemático griego de la escuela de Alejandría.
Redactó trece libros de aritmética y uno de números angulares. Desarrollo una teoría innovadora acerca de las ecuaciones de primer grado y propuso formas de resolución de las de segundo grado.
Euclides (c.3000 a. C)
Matemático griego fundador de la escuela de Alejandría. Además de sus aportaciones a otros campos del saber como la óptica, su principal obra fue llamada Elementos, considerada la obra de geometría por excelencia, y que contiene el famoso postulado que lleva su nombre.
Arquímedes (287 a. C.- 212 a. C.)
Sabio griego. Discípulo de Euclides, además de sus importantes de carácter físico (p.ej. las leyes de la palanca) y técnico (tornillo, sin fin, polea móvil, ruedas dentadas, etc.), desarrollo un método para obtener el número pi, perfeccionó el sistema numérico griego y realizo notables contribuciones en el campo de la geometría.
Eratóstenes (c. 284 a. C.- c.192 a.C.)
Astrónomo, filósofo, geógrafo y matemático. Además de ser el primero en medir de forma exacta la circunferencia de la Tierra, creó la criba que lleva su nombre, para la obtención de los números primos, y un instrumento para resolver el problema de la media proporcional (mesolabio).
Fermat, Pierre de (1601-1665)
Matemático francés. Se le reconoce el mérito de haber expresado las primeras idea acerca de cálculo diferencial y algunos autores le reconocen la paternidad del cálculo de probabilidades, compartida con Pascal. Entre sus creaciones destacan el principio, el teorema y el último teorema que llevan su nombre.
Pascal, Blaise (1623-1662)
Matemático, físico, filósofo y escritor francés. Aparte de importantes resultados en el estudio de las cónicas, cicloides y primeros esbozos del cálculo infinitesimal, se le deben contribuciones fundamentales en diversos campos de la física (estudio del vacío, estática de líquidos, etc.), la construcción de varios ingenios mecánicos de cálculo (pascalinas) y la formulación de las bases del cálculo de probabilidades.
Newton,sir Isaac (1642-1727)
Físico, matemático y astrónomo británico.
Sus importantes contribuciones a los campos de las matemáticas y la física incluyen, entre otros, el llamado cálculo de fluxiones (cálculo infinitesimal cuya paternidad le disputa Leibniz) y la sistematización de la mecánica clásica, así como la formulación de las leyes de la gravitación universal.
Goldbach, Christian (1690-1764)
Matemático alemán.sus trabajos se centraron en la teoría de series y sus aplicaciones a la integración de ecuaciones diferenciales. Planteó el problema que lleva su nombre (1742) y que fue resuelto en 1937 por Vinogradov, y propuso la conjetura de Goldbach, aún no resuelta.
Euler, Leonhard (1707-1783)
Matemático suizo.Fue el más famoso de la familia de matemáticos a la que perteneció.
Entre sus obras destacan su Tratado completo de mecánica (aplicación del análisis matemático al movimiento), su teoría del movimiento de los planetas y cometas y, sobre todo, su Introducción al análisis de infinitésimos (1748)y sus Instituciones de cálculo integral (1755), consideradas clásicas.
Clairaut. Alexis (1713-1765)
Matemático y astrónomo francés. Además de participar en la expedición a Laponia para la mediad del meridiano terrestre y calcular el regreso del cometa Halley (1758), hizo contribuciones a la llamada teoría de los tres cuerpos y, en el campo de las matemáticas, al llamado análisis superior.
Lagrange, conde Louis de (1736-1813)
Matemático francés. Además de sus aportaciones el cálculo de variaciones y al cálculo integral, como la introducción de un simbolismo más cómodo para éste, se le debe una obra fundamental titulada Mecánica analítica (1788)
Fundamentó el análisis sobre una noción más general de función, en particular mediante el empleo de desarrollos en serie de Taylor.
Definió las funciones derivadas e introdujo una notación especial para expresarlas.
Gauss, Carl- Friedrich (1777-1855)
Astrónomo, matemático y físico alemán.
Además de sus importantes trabajos en los campos de la astronomía y la física, escribió u tratado sobre la teoría de los números, ideó el método de los mínimos cuadrados, creó la teoría de errores hizo aportaciones notables en el campo de las curvas y desarrolló un método general de resolución de ecuaciones binomias.
Bolzano, Bernhard (1781-1848)
Filósofo, lógico y matemático checo de origen italiano. Además de sus importantes trabajos en el campo de los fundamentos de la lógica, anticipo importantes concepciones relativas a la teoría de conjuntos y creó la primera función continua no diferenciable en ningún punto.
Cauchy, barón Augustin (1789-1857)
Matemático francés. Autor de más de setecientas memorias en diversos campos de la ciencia, introdujo métodos rigurosos en el campo del análisis y creó la llamada teoría de las funciones analíticas.
Abel, Niels Henrik. (1802-1829)
En el campo del análisis matemático está considerado, junto con Jacobi, como el creador de la teoría de funciones elípticas. Formuló, en un trabajo presentado ante la Academia de Ciencias de París, el teorema que lleva su nombre.
Dirichlet, Gustav Lejeume (1805-1859)
Matemático alemán. Sus principales aportaciones (fundamentales para la física matemática) se refieren alas series e integrales trigonométricas y al campo de la teoría de ecuaciones en derivadas parciales, así como a una rama abstracta de las matemáticas como la teoría de los números.
Galois, Evariste (1811-1832)
Matemático francés, Formuló una teoría de las ecuaciones matemáticas, recogiendo los resultados relativos a la clasificación y periodicidad de las integrales abelianas. Su principal aportación se centra en la importancia de los grupos en la resolución de ecuaciones algebraicas.
Boole, George (1815-1864)
Lógico y matemático británico. Se le debe la introducción del cálculo algebraico en le campo de la lógica y el cálculo de clases conocido como algebra de Boole de las clases.
Heine, Heinrich Eduard (1821-1881)
Matemático alemán. Heine hizo sus principales contribuciones de las matemáticas en el campo del análisis (polinomios de Legendre, funciones de Bessel y Lamé, etc. Su resultado más famoso es el llamado teorema de Heine- Borel.
Kronecker, Leopold (1823-1891)
Matemático alemán. Considerado uno de los mayores algebristas del siglo XIX , estudió, entre otras las funciones elípticas en aritmética y la teoría de cuerpos de los números algebraicos.
Riemann, Georg Friedrich Bernhard (1826-1866)
Matemático alemán. Además de sus contribuciones a la física matemática, hizo aportaciones a la teoría de funciones y enunció los fundamentos de la geometría diferencial para espacios de dimensión superior a tres. Formuló la teoría de las funciones abelianas e introdujo la llamada función z, lo que permitió obtener resultados notables relativos a los números primos.
Dedekind, Richard (1831-1916)
Matemático alemán. Alumno de Gauss, e introductor en el campo del análisis de las nociones que permiten precisar el concepto de número inconmensurable, se le deben trabajos relativos, entre otros, a las integrales eulerianas, a los números irracionales, a las ecuaciones y funciones algebraicas, etc.
Frege, Gottlob (1848-1952)
Filósofo, lógico y matemático alemán. Considerado el fundador de la lógica moderna o matemática, cuyos trabajos tuvieron una notable influencia en pensadores como Carnap, Husserl y Wittgenstein.
Cantor, Georg (1854-1948)
Matemático alemán de origen ruso. Se le considera el creador de la llamada teoría de conjuntos y de la teoría de los números transfinitos. Su obra impulsó una revisión en profundidad de los fundamentos de las matemáticas.
Poincaré, Henri (1854-1912)
Matemático francés, es autor de contribuciones fundamentales en los campos de la teoría de funciones, las ecuaciones diferenciales y sus aplicaciones a los problemas de la mecánica celeste, y el estudio de problemas de física matemática(p. ej., teoría de las ondas electromagnéticas).
Peano, Giuseppe (1858-1932)
Lógico y matemático italiano. Además de la exposición rigurosamente deductiva de diversos campos de las matemáticas, creó un sistema de de símbolos para la descripción y enunciado de las proposiciones lógicas y matemáticas sin necesidad de recurrir al lenguaje ordinario.
Whitehead, Alfred North (1861-1947)
Filósofo y matemático británico. Además de sus fundamentales aportaciones en el campo de la filosofía, está considerado como uno de los de la lógica matemática.
Hilbert, David (1862-1943)
Matemático alemán. Se le debe la formulación de la noción de cuerpo y la creación de la teoría de los cuerpos para los números algebraicos. Desarrolló los fundamentos de la llamada teoría de invariantes y estableció las bases de la teoría de prototipos de polinomios. Sus fundamentos de geometría (1899) están considerados el punto de partida de la axiomatización de varias ramas de las matemáticas.
Hadamard, Jacques (1865-1963)
Matemático francés. En la vasta obra que produjo gracias a su longevidad, destacan sus importantes investigaciones relativas ala distribución de los números primos, al análisis funcional término acuñado por Hadamard), así como sus resultados relativos a la teoría de números.
De la Vallée- Pousin, Charles Jean Gustave Nicolas (1866-1692)
Matemático belga. Realizo importantes trabajos relativos a las ecuaciones diferenciales a la función z de Riemann y fue autor de un famoso curso de análisis. Su resultado más importante fue el teorema de los números primos.
Russel, Bertrad Arthur William tercerconde (1872-1970)
Filósofo matemático y sociólogo inglés. Creador del logicismo y de la llamada teoría de los tipos, además de sus aportaciones fundamentales a la filosofía del conocimiento, destacan sus contribuciones en los campos de la matemática, la filosofía de la ciencia, la teoría del conocimiento, etc.
Carathédory, Constantin (1873-1950)
Matemático grecogermano. Se le deben importantes contribuciones, entre otras, en los campos del cálculo de variaciones, la teoría de la medida y los problemas teóricos relacionados con las funciones.
Lebesque, Henri (1875-1941)
Matemático francés. Además de sus trabajos sobre teorías de funciones de variable real, es autor, entre otros logros, de una generalización de la noción de integral que lleva su nombre.
Hardy, G (odfrey). H (arold). (1877-1947)
Matemático Británico. Su vasta obra abarca la teoría de números, cuestiones de análisis puro y la teoría de funciones. En colaboración con Littlewood y Rosser obtuvo valores asintóticos para las series o productos finitos relacionados con los números primos, como por ejemplo la serie de sus inversos.
Fatuo, Pierre Joseph Louis (1878-1929)
Matemático francés. Además de sus estudios acerca de las series de Taylor y la integral de Lebesque, se le deben importantes trabajos relativos al movimiento planetario en medios resistentes.
Littlewood, John Edensor (1885-1977)
Matemático británico. Hizo aportaciones a la teoría de series, en colaboración con G.H Hardy, y público diversos trabajos basados en la aplicación del llamado método analítico Hardy- Littlewood- Ramanujan.
Ramanujan, Srinivasa (1887-1920)
Matemático indio. Con la ayuda de G.H Hardy se traslado a Inglaterra, donde escribió importantes artículos sobre la teoría analítica de los números. Sus descubrimientos tuvieron gran influencia en la física moderna (teoría de supercuerdas) y en el campo de la estadística de los sistemas moleculares.
Von Neuman, Johann o John (1903-1957)
Matemático estadounidense de origen húngaro. Fundamentalmente se le deben contribuciones muy notables a la teoría de conjuntos, a la teoría de juegos y al desarrollo de máquinas de calcular electrónicas.
Oppenheimer, Robert Julios (1904-1967)
Físico estadounidense. Realizó importante trabajos en los campos de la física atómica y la teoría cuántica. Dirigió la creación de la bomba atómica en Los Álamos (1943-1945).
Princeton (1947-1966) y se opuso a la construcción de la bomba de hidrógeno, por lo que obtuvo represalias.
Tichonov, Andréi Nikoláievich(1906-1993)
Matemático ruso. Destacó por sus trabajos en el campo de la topología y análisis funcional, en la teoría de ecuaciones diferenciales y en problemas de matemática computacional y física matemática.
Godel, kart (1906-1978)
Lógico estadounidense de origen austriaco. En su tesis relativa a los fundamentos lógico matemáticos, estableció la completitud del llamado cálculo de predicados. Si embargo, goza de fama mundial por la formulación de sus dos teoremas de incompletitud, que afirman que no puede demostrarse la completitud de la teoría matemática utilizando únicamente procedimientos formalizables en el seno de dicho sistema.
Weil, André (1906-1998)
Matemático francés. Contribuyó al avance de la geometría y la teoría de números estableciendo las bases de la geometría algebraica abstracta y de la moderna teoría de variedades abelianas . Sus trabajos sobre curvas algebraicas han tenido gran influencia incluso en la física moderna.
Turing. Alan Mathison (1912-1954)
Matemático británico. Hizo notables contribuciones en los campos de la lógica matemática, teoría de grupos, inteligencia artificial y máquinas de calcular. Se le debe asimismo la formulación de la llamada máquina de Turing.
Sumatoria
El sumatorio, la sumatoria, o la operación de suma es un operador matemático que permite representar sumas de muchos sumandos, n o incluso infinitos sumandos, se expresa con la letra griega sigma (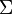
), y se define como:
La variable i es el índice de suma al que se le asigna un valor inicial llamado límite inferior, m. La variable i recorrerá los valores enteros hasta alcanzar el límite superior, n. Necesariamente debe cumplirse que:
Limite
En muchas ocasiones algunas frases conducen de manera intuitiva a la definición de limite, tales como: “Se aproxima a un número específico”, “x se aproxima hacia a”, “f(x) se hace arbitrariamente grande”. Desde Leibnitz, Newton en el siglo XVII a través de los Bernoulli, Euler y Gauss en el siglo VIII y hasta principios del siglo. Sin embargo, a medida que el tiempo transcurría la definición intuitiva de límite necesitaba de librarse de su origen “los objetos móviles” y simples gráficas. Fue Weierstrass, alrededor de 1841 a 1856 quien desarrollo un método para definir los límites si hacer alusión a lo anterior. Desde entonces este método ha sido usado tanto por matemáticos puros y aplicados Weierstrass.
Sea f(x) una función y a un número fijo.
Supongamos que el codominio de f contiene intervalos abiertos (c,a) y (a,b), para algún número c<a y algún número b>a, como en la figura (G.1).
Si al aproximarse x hacia a, tanto por su izquierda como por su derecha (esto también es equivalente a decir que existe tanto el limite de la función tanto por la izquierda como por la derecha), f(x) tiende a un número específico S, entonces S se llama el límite de f(x) cuando x tiende hacia a.
Lo cual se representa de la siguiente forma:
Entonces podemos determinar los limites para algunas funciones.
Derivada
Históricamente el concepto de derivada es debido a Newton y a Leibnitz. Sus definiciones surgen a raíz del concepto de limite.
Sin embargo, son varias las formas en que se ha generado el concepto de derivada, los comunes son los siguientes:
Definición: Pendiente de una curva. La pendiente del gráfico de la función f en el punto
(x , f(x) ) es la derivada de f en x.
Definición: Tangente a una curva. La recta tangente al grafico de la función f en el punto
P = (x , f(x) ) es la recta que pasa por P con pendiente igual a la derivada de f en x.
Definición: Velocidad de una partícula que se mueve sobre una línea recta. La velocidad en el instante t de un objeto, cuya posición sobre una recta viene dada por f(t) en el instante t, es la derivada de f en el punto t. El valor absoluto de la velocidad es el módulo de esa cantidad.
Definición: Amplificación de una proyección entre rectas. La amplificación en x de una lente que proyecta el punto x de una recta sobre el punto f(x) de otra recta es la derivada de f en x.
Definición: Densidad de un material. La densidad de x de un material distribuido a lo largo de una recta de forma tal que los x centímetros de la izquierda tengan una masa de f(x) gramos es igual a la derivada de f en x.
Una forma clásica de construir el concepto de derivada es la segunda definición, la de recta tangente a una curva, podríamos iniciar por tomar una línea que corta a la gráfica de la función en mas de un punto, como se muestra a continuación:
a medida que los intervalos de posición en x son mas pequeños como el esquema que se muestra a continuación, la línea recta tiende a ser mas semejante a una línea tangente que a una línea recta secante:
Analizando esta línea tangente podemos ver que:
el triángulo rectángulo que se forma puede conducirnos a analizar cual es la ecuación de la pendiente de la línea recta tangente. Nótese la hipotenusa dentro del triangulo rectángulo corresponde a la línea recta.
Como podemos apreciar la ecuación que relaciona la línea recta esta dada por la tangente:
pero como sabemos para la línea recta dicha relación nos da la pendiente de una línea recta
Como hemos dicho esta relación, de recta tangente se logra solo que los intervalos:
sean pequeños lo que equivale a decir que se genera el limite cuando 
o lo que equivale a decir que se genera el limite:
fue a ese limite al que se le dio el nombre de derivada:
donde 
es una notación para indicar el operador de derivada.
es una notación para indicar el operador de derivada.
Nota: Como podremos ver 
sin embargo no debe de tomarse como la operación de dividir dx entre dx.
sin embargo no debe de tomarse como la operación de dividir dx entre dx.Conclusión
El progreso de las ideas no se da en el tiempo a través de una trayectoria perfectamente delineada y preconcebida; existen muchos elementos que en la construcción son desechados, reformulados o agregados. Las concepciones filosóficas sobre la realidad, el papel de la ciencia, y en especial las concepciones sobre las características que debe reunir el conocimiento matemático para ser considerado como conocimiento científico, determinaron los enfoques realizados en cada época. El impacto que tuvieron los personajes y las contribuciones consignadas en la historia difícilmente puede ser comprendida cabalmente si estas consideraciones no se toman en cuenta.
